Romain Leconte (École Normale Supérieure – PSL, UMR 8097 Centre Maurice Halbwachs)
Feuille 2024-1 : Télécharger la Feuille
Objectifs
- Formaliser un réseau par un graphe
- Comprendre et utiliser les indicateurs globaux et locaux pour décrire un graphe
Description du cours
Type : Feuille de cours
Niveau : Licence
Durée : 1 séance de 2h30 à 3h
Mots-clefs : Analyse spatiale, graphe, réseau, centralité, jeu
Remarques : Les étudiant.es doivent être familier.e.s du formalisme des matrices de relations spatiales avant la mise en œuvre de cette activité. Cette activité a été mise en œuvre avant la pandémie de Covid-19.
Cette expérience pédagogique a été mise en œuvre avec la complicité de Marianne Guérois et Luc Guibard (Université de Paris Cité, UMR 8504 Géographie-cités)
Pour citer cette Feuille
Romain LECONTE, 2024. “Jouer avec les réseaux : initiation à l’analyse de graphe à partir du jeu de plateau Pandemic”, Feuilles de Géographie, 2024-1, nombre de pages.
Jouer avec les réseaux : initiation à l’analyse de graphe à partir du jeu de plateau Pandemic
Les réseaux sont un type d’objet transversal aux différents champs de la géographie. Ils peuvent être réseaux viaires et de transport, réseaux écologiques, réseaux sociaux, d’entreprises ou d’institutions ou encore réseaux sémantiques. Le réseau caractérise un ensemble varié de relations entre différents types d’individus qui peuvent être localisés dans l’espace géographique. On parle alors de réseau spatial. Les réseaux peuvent être formalisés par un graphe, un objet mathématique composé d’un ensemble de sommets (ou nœuds), et d’un ensemble de paires de sommets, les arrêtes (ou liens). La théorie des graphes offre des outils commodes pour décrire et comparer la structure des graphes, ou pour caractériser la position relative des sommets dans le graphe, on parle alors de centralité des sommets.
L’initiation des étudiant·es aux méthodes d’analyse des graphes implique de montrer comment un réseau géographique quelconque peut être transformé en une matrice de relations spatiales, un objet familier du traitement de l’information géographique, et d’expliquer les outils statistiques propres à son analyse. Pour autant, ces deux démarches présentent des difficultés. Autant la transformation d’un réseau matériel en graphe parait évidente tant nous sommes familiers de ces représentations avec les plans de métro, autant les réseaux immatériels sont encore plus abstraits quand ils sont visualisés sous la forme d’un graphe ou d’une matrice, qui ne permettent pas de retranscrire les positions dans l’espace géographique (distances et localisations). De même, la traduction de la notion commune de centralité en une déclinaison d’indicateurs aux différentes propriétés peut amener de la confusion dans leur intérêt respectif.
Jouer à Pandemic est ainsi apparu comme un moyen intuitif d’analyser un graphe. Les joueurs sont amenés à comprendre la structure du graphe et à comparer la centralité des nœuds pour affiner leur stratégie de jeu. Pandemic est un jeu de plateau coopératif où les joueurs doivent empêcher le développement de pandémies. Le plateau est constitué de villes qui sont susceptibles d’être contaminées de manière aléatoire. Les villes sont reliées entre elles par des segments qui permettent aux joueurs de se déplacer et à la maladie de se propager. Les joueurs doivent se déplacer dans le graphe et user de la compétence spécifique du personnage qu’ils incarnent pour lutter contre la progression de quatre maladies à travers les villes du monde. Sans entrer dans le détail des règles (cf. proposition d’accompagnement pédagogique), trois actions sont particulièrement intéressantes dans le jeu :
- créer de nouveaux liens entre les villes (action « Construire une station de recherche ») qui peuvent être empruntés pour se déplacer sur le plateau ;
- positionner le personnage du « Médecin » sur une ville : celui-ci peut éradiquer la maladie dans la ville. C’est donc la capacité du médecin à atteindre rapidement les villes contaminées qui va permettre de contrôler le développement des épidémies ;
- positionner le personnage « Spécialiste mise en quarantaine » sur une ville : celui-ci empêche le développement de l’épidémie dans la ville où il se trouve ainsi que dans toutes les villes qui lui sont directement reliées.
Le jeu en géographie est un outil pédagogique mobilisé dans de nombreux contextes, pour l’initiation des étudiant·es aux principes fondamentaux des localisations[1] ou au service de la concertation et la participation citoyenne dans la planification territoriale[2]. Le jeu fait l’objet d’innovations et réflexions pédagogiques régulières (Ter Minassian et S. Rufat, 2008 ; Oiry, 2018)[3] et peut avoir un intérêt spécifique en analyse spatiale. Ainsi, H. Ter Minassian et S. Rufat (2008) écrivent à propos des jeux vidéos :
« La construction d’un modèle est une représentation de la réalité, une abstraction plus ou moins formalisée en langage logique, sous forme de récit littéraire, de carte géographique ou d’équation mathématique. Comme tout processus d’acquisition cognitive aboutit à un modèle, le déroulement d’une partie de jeu vidéo conduit le joueur à s’approprier ces modèles en analysant la façon dont la simulation répond à ses choix et décisions. La simulation informatique permet d’éviter le double écueil de la simplicité réductrice et de la trop grande complexité : elle ouvre un niveau de réflexion abstraite « intermédiaire », parce que les modèles ne sont pas donnés a priori et que la formalisation reste « cachée » derrière l’interface graphique. »
Cette affirmation peut être transférée au cas spécifique de l’enseignement de la théorie des graphes avec Pandemic : le plateau de jeu modélisant le Monde constitue un niveau de formalisation intermédiaire permettant la transition de la complexité des interactions spatiales entre villes à la simplification d’une matrice topologique. Par ailleurs, le déroulé de la séquence permet de mettre en forme mathématique les intuitions des étudiant·es qui auront amélioré la connexité du réseau et se seront positionnés sur les nœuds selon différents indicateurs de centralité de manière spontanée. Cela peut lever quelques réticences vis-à-vis de la quantification.
[1] Jeu conçu par Ch. Grataloup et édité par le CNDP en 1989 dans La Géographie dans tous ses états et disponible en ligne : http://www.ac-grenoble.fr/histoire/didactique/general/jeux/villes/index.htm.
[2] « La ville sous cloche », jeu conçu par A. de Lajatre et M. Gigot autour des l’élaboration des documents d’urbanisme : https://centrejeanbodin.univ-angers.fr/fr/les-projets/projets-en-cours-2/la-ville-sous-cloche.html?search-keywords=ville+sous+cloche
[3] On pourra se reporter à la bibliographie de Ter Minassian et Rufat, 2008.
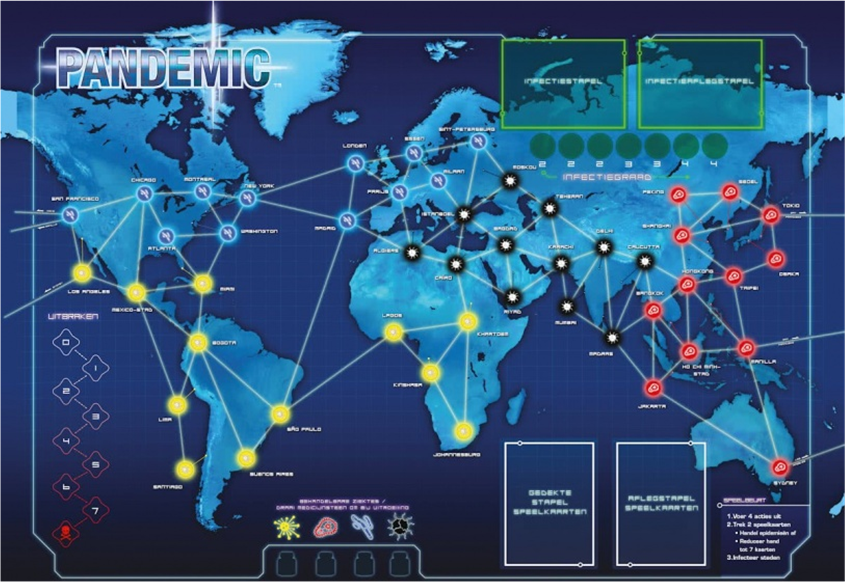
Déroulé d’une partie
1. Les étudiant·es, par groupe, jouent une partie de Pandemic

2. Les étudiant·es affinent leur stratégie en analysant le graphe

Support de cours
Jeu Pandemic
Auteur : Matt Leacock
Illustrations : Chris Quilliams
Edition : Filosofia
Règles du jeu : https://cdn.1j1ju.com/medias/f8/5d/96-pandemic-regle.pdf
Questions :
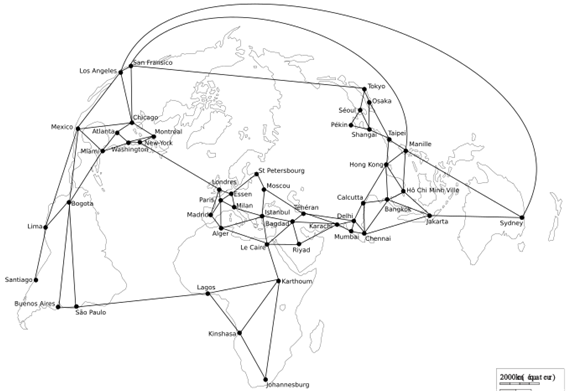
1. A l’aide de la théorie des graphes, caractériser l’évolution globale du réseau entre la situation 1 (figure 1) et la situation 2 (figure 2).
- Sur la figure 2, reliez les villes équipées d’un centre de recherche entre elles.
- Définissez les différents indicateurs de connectivité. Complétez le tableau 1. Qu’observez-vous ?
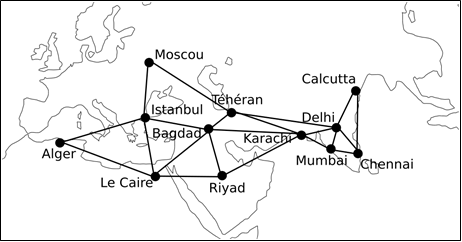
2. Comparez l’accessibilité des villes noires (figure 3).
- Complétez la matrice des plus courts chemins (tableau 2)
- Calculez les indicateurs locaux de position (tableau 3) : déterminez quelles villes sont les plus et les moins accessibles.
- Quel indicateur d’accessibilité retenir pour localiser de façon optimale :
- le « spécialiste mise en quarantaine » devant empêcher la diffusion des épidémies
- le « médecin » devant se rendre dans les villes en cas de contamination

| Situation | L | S | C | β | γ | μ | α |
| 1 | |||||||
| 2 |
| ALG | BAG | CAL | CHE | DEL | IST | KAR | LEC | MOS | MUM | RIY | TEH | Total | |
| ALG | 2 | 5 | 5 | 4 | 1 | 3 | 1 | 2 | 4 | 2 | 3 | 32 | |
| BAG | 2 | 3 | 3 | 2 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 19 | |
| CAL | 5 | 3 | 1 | 1 | 4 | 2 | 4 | 3 | 2 | 3 | 2 | 30 | |
| CHE | 5 | 3 | 1 | 1 | 4 | 2 | 4 | 3 | 1 | 3 | 2 | 29 | |
| DEL | 4 | 2 | 1 | 1 | 3 | 1 | 3 | 2 | 1 | 2 | 1 | 21 | |
| IST | 1 | 1 | 4 | 4 | 3 | ||||||||
| KAR | 3 | 1 | 2 | 2 | 1 | ||||||||
| LEC | 1 | 1 | 4 | 4 | 3 | ||||||||
| MOS | 2 | 2 | 3 | 3 | 2 | ||||||||
| MUM | 4 | 2 | 2 | 1 | 1 | ||||||||
| RIY | 2 | 1 | 3 | 3 | 2 | ||||||||
| TEH | 3 | 1 | 2 | 2 | 1 | ||||||||
| Tot. | 32 | 19 | 30 | 29 | 21 | 286 |
| ALG | BAG | CAL | CHE | DEL | IST | KAR | LEC | MOS | MUM | RIY | TEH | |
| CD | ||||||||||||
| CE | ||||||||||||
| CM |
Proposition d’accompagnement pédagogique
Quatre maladies se propagent dans le Monde. L’équipe de joueur·euses est composée de 2 à 7 personnages qui doivent allier leurs capacités individuelles pour lutter contre les épidémies avant qu’elles ne ravagent le Monde.
A chaque tour, un·e joueur·euse peut mener 4 actions pour se déplacer sur le plateau et lutter contre la maladie. Mais à chaque tour, l’épidémie peut s’accélérer brutalement si une carte « Épidémie » est piochée. Il faut donc que les joueur·euses développent une stratégie collective pour traiter la maladie plus vite qu’elle ne se développe.
Les actions menées par les joueur·euses sont spatialement contraintes : ils·elles doivent se déplacer sur le plateau en empruntant les segments qui relient les villes entre elles, se rendre dans la ville infectée pour pouvoir la traiter, se rendre dans des villes équipées de stations de recherche pour découvrir un remède etc. C’est donc cette contrainte spatiale que les joueur·euses vont devoir s’approprier pour lutter contre les épidémies. Cela passe par une optimisation des déplacements dans le graphe et une amélioration de la connectivité du graphe, en créant de nouveaux liens entre les villes. Cette stratégie spatiale ne doit pas être révélée aux étudiant·es au préalable ; l’objectif est de la faire émerger au cours de la partie.
D’autre part, les joueurs ont des rôles dotés de propriétés spatiales propres qu’ils peuvent mobiliser pour lutter contre l’épidémie.
- La « spécialiste mise en quarantaine » empêche le développement des maladies dans les villes où elle se trouve et dans toutes les villes qui lui sont directement reliées.
- Le médecin peut éliminer la maladie dans la ville où il se trouve.
- La scientifique peut découvrir un remède dans une station de recherche etc.
Il y a donc une stratégie de localisation des personnages dans le graphe à développer pour utiliser au mieux leurs compétences spécifiques.
La partie s’achève lorsque les maladies ont atteint le stade pandémie ou qu’elles ont été complètement éradiquées par l’équipe de joueur·euses.
| La mise en place de cet exercice nécessite pour l’enseignant·e de se familiariser au préalable avec le jeu.Pour raccourcir le temps de jeu, on pourra opter pour le niveau de jeu le plus difficile, avec 6 cartes épidémie [cf. Règles du jeu / Mise en place / Préparez le paquet Joueur]La présence du médecin et de la spécialiste mise en quarantaine parmi les personnages de la partie est indispensable.Il s’agit d’un jeu collaboratif, tous·tes les étudiant.es jouent ensemble contre l’épidémie : on peut donc dépasser sans crainte le nombre de joueur·euses indiqué. Un personnage peut être incarné par deux ou trois étudiant·es. On pourra nommer un·e maître du jeu parmi les étudiant·es qui aura pour rôle de veiller au respect des règles du jeu. |
La séance débute par une partie jouée en autonomie par les étudiant·es. Deux possibilités d’enseignement peuvent être imaginées : soit une séance introduisant les notions fondamentales de l’analyse de graphe (centralité, connexité…) aura eu lieu au préalable, soit la partie de jeu servira à introduire ces notions en répondant aux questions du support de cours.
A la fin de la partie, on pourra formuler des hypothèses avec les étudiant·es sur les causes de leur défaite ou de leur victoire relatives au positionnement des personnages sur le plateau ou aux déplacements effectués.
1. A l’aide de la théorie des graphes, caractériser l’évolution globale du réseau entre la situation 1 (figure 1) et la situation 2 (figure 2).
Cette comparaison de la structure du réseau entre le début et la fin de la partie s’appuie sur le fait que les étudiant·es ont établi de nouveaux liens entre les villes en créant des stations de recherche. On abordera ici les indicateurs globaux de connexité et de connectivité.
- Sur la figure 2, reliez les villes équipées d’une station de recherche entre elles.
Cette question est l’occasion de définir quatre propriétés du graphe à partir de leur observation :
- la connexité : tous les sommets sont ici reliés à chacun des autres sommets par une chaîne de segments, il s’agit donc d’un graphe connexe (une seule composante). C’est un paramètre qui entrera dans le calcul des indicateurs globaux.
- la planarité : un graphe planaire est un graphe où aucune des arrêtes ne se croisent. C’est le cas de la situation 1. Il est fort probable que la création de nouveaux liens rende le graphe non planaire. Cette distinction est très importante pour le calcul des indicateurs suivants. Un graphe est planaire si L ≤ 3S – 6 et non planaire si L > 3S – 6
- l’orientation : il s’agit ici d’un graphe non orienté, les personnages peuvent se déplacer dans un sens ou dans l’autre sur les segments.
- la valeur des liens : il s’agit ici d’un graphe non valué, chaque segment coûte une action à parcourir, quelle que soit sa longueur sur la carte.
- Complétez le tableau 1. Qu’observez-vous ?
| Situation | L | S | C | β | γ | μ | α |
| 1 | 86 | 48 | 1 | 1,79 | 0,62 | 39 | 0,43 |
| 2 | 48 | 1 |
Pour compléter le tableau, on dénombrera le nombre de sommets (S – villes), qui n’évolue pas d’une situation à l’autre, le nombre de liens (L – qui aura augmenté) et le nombre de composantes connexes (C = 1, stable). Ce sont les dimensions du graphe.
Avant toute chose, il faut déterminer si le graphe de la situation 2 est toujours planaire. S’il ne l’est plus, on comparera les indicateurs standardisés qui prennent pour dénominateur les valeurs maximales d’un graphe non planaire.
Les deux graphes étant connexes, on calcule directement les indicateurs globaux de connectivité qui mesurent la densité des relations entre les sommets d’un graphe, à partir de la fréquence des liens. Un graphe très connexe présente de nombreux chemins alternatifs pour se rendre d’un sommet à un autre.
Indicateur Beta (β) : β = L / S
β exprime le rapport entre le nombre de liens et le nombre de sommets. Cet indice ne permet pas de comparer deux graphes de taille différente (en nombre de sommets), parce que son maximum dépend du nombre de sommets. Mais ici, le nombre de villes étant fixe, il peut être utilisé.
Indicateur Gamma (γ) : γ = L / Lmax = L / 3(S – 2) ou L / (((S^2 – S) / 2))
γ est une version standardisée de β évoluant entre 0 et 1. Il exprime le rapport entre le nombre de liens observé et le nombre maximal de liens possibles. Le nombre maximal de liens dépend de la nature du graphe. Un graphe planaire non orienté a pour nombre maximal de liens 3(S-2). Pour un graphe non planaire non orienté, le nombre maximal de liens est de (S²-S)/2.
Indicateur cyclomatique (γ) : μ = L – S + C
μ (indicateur cyclomatique) exprime le nombre maximal de circuits indépendants que l’on peut parcourir simultanément à l’intérieur d’un graphe. Un circuit est une chaîne dont le premier sommet coïncide avec le dernier, et que l’on peut parcourir sans emprunter deux fois le même segment. Cet indicateur ne peut pas être utilisé lorsque les réseaux sont de taille différente.
Indicateur Alpha (α) : α = μ / μmax = (L – S + C) / (2S – 5) ou (L – S + C) / (( (S^2 – S) / (2 – (S – 1))))
α est une version standardisée de μ évoluant entre 0 et 1. Il exprime le rapport entre le nombre observé de circuits indépendants et le nombre maximal de circuits indépendants. Dans les graphes planaires, le nombre maximal de circuits est égal à (2S-5). Pour un graphe non planaire non orienté, le nombre maximal de circuits est de (S²-S)/2-(S-1).
Du point de vue du jeu, on pourra comparer les groupes d’étudiant·es pour savoir lequel d’entre eux a fait le plus progresser la connectivité du graphe.
2. Comparez l’accessibilité des villes noires (figure 3).
Cette partie de l’exercice s’appuie sur un extrait du graphe afin que celui-ci soit planaire et que la matrice soit de petite taille, et facilement manipulable à la main.
- Complétez la matrice des plus courts chemins (tableau 2).
L’accessibilité mesure la facilité à atteindre un nœud au sein d’un réseau. C’est un indicateur très important à prendre en compte pour déplacer l’équipe de personnages qui lutte contre l’épidémie. Pour déterminer l’accessibilité d’un sommet dans un graphe, on calcule des indicateurs de centralité ou indicateurs locaux/de position. Les mesures de centralité impliquent de construire une matrice des plus courts chemins. Elle exprime en distance topologique (1 lien est égal à 1 unité de distance) la distance la plus courte pour rejoindre deux sommets du graphe.
| ALG | BAG | CAL | CHE | DEL | IST | KAR | LEC | MOS | MUM | RIY | TEH | Total | |
| ALG | 2 | 5 | 5 | 4 | 1 | 3 | 1 | 2 | 4 | 2 | 3 | 32 | |
| BAG | 2 | 3 | 3 | 2 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 19 | |
| CAL | 5 | 3 | 1 | 1 | 4 | 2 | 4 | 3 | 2 | 3 | 2 | 30 | |
| CHE | 5 | 3 | 1 | 1 | 4 | 2 | 4 | 3 | 1 | 3 | 2 | 29 | |
| DEL | 4 | 2 | 1 | 1 | 3 | 1 | 3 | 2 | 1 | 2 | 1 | 21 | |
| IST | 1 | 1 | 4 | 4 | 3 | 2 | 1 | 1 | 3 | 2 | 2 | 24 | |
| KAR | 3 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 18 | |
| LEC | 1 | 1 | 4 | 4 | 3 | 1 | 2 | 2 | 3 | 1 | 2 | 24 | |
| MOS | 2 | 2 | 3 | 3 | 2 | 1 | 2 | 2 | 3 | 3 | 3 | 24 | |
| MUM | 4 | 2 | 2 | 1 | 1 | 3 | 1 | 3 | 3 | 2 | 2 | 24 | |
| RIY | 2 | 1 | 3 | 3 | 2 | 2 | 1 | 1 | 3 | 2 | 2 | 22 | |
| TEH | 3 | 1 | 2 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 2 | 19 | |
| Tot. | 32 | 19 | 30 | 29 | 21 | 24 | 18 | 24 | 24 | 24 | 22 | 19 | 286 |
- Calculez les indicateurs locaux de position (tableau 3) : déterminez quelles villes sont les plus et les moins accessibles.
| ALG | BAG | CAL | CHE | DEL | IST | KAR | LEC | MOS | MUM | RIY | TEH | |
| CD | 2 | 5 | 2 | 3 | 5 | 4 | 5 | 3 | 2 | 3 | 3 | 4 |
| CE | 2,9 | 1,73 | 2,73 | 2,63 | 1,9 | 2,1 | 1,64 | 2,18 | 2,45 | 2,18 | 2 | 1,73 |
| CM | 5 | 3 | 5 | 5 | 4 | 4 | 3 | 4 | 3 | 4 | 3 | 3 |
La centralité de degré (CD) exprime le nombre de liens qui partent d’un sommet. On peut la déterminer en comptant pour chaque ville le nombre de 1 dans la matrice.
La centralité d’éloignement moyen (CE) exprime la distance moyenne entre un sommet et l’ensemble des autres sommets.
La centralité d’éloignement maximal (CM) exprime la distance maximale entre un sommet et l’ensemble des autres sommets.
Les villes qui ont une centralité de degré élevée sont dans une position de carrefour. La centralité d’éloignement moyen permet de déterminer quelles sont les villes les plus accessibles depuis l’ensemble des autres villes. La centralité d’éloignement maximal permet de déterminer quelles sont les villes les plus accessibles depuis les villes les plus éloignées ou périphériques. Ces indicateurs ne seront alors pas utilisés de la même manière en fonction des capacités de chacun des personnages du plateau.
- Quel indicateur d’accessibilité retenir pour localiser de façon optimale :
- le « spécialiste mise en quarantaine » devant empêcher la diffusion des épidémies
On positionnera ce personnage en priorité sur les villes qui ont une forte centralité de degré puisqu’il peut protéger les villes qui lui sont directement reliées. Plus la centralité de degré est élevée, plus le personnage protégera de nombreuses villes.
- le « médecin » devant se rendre dans les villes en cas de contamination
On positionnera ce personnage sur les villes où la centralité d’éloignement moyen est la plus faible. De là, il pourra atteindre un maximum de villes du réseau avec un faible coût de déplacement. C’est là qu’il sera le plus efficace. En revanche, les villes les plus périphériques peuvent être lésées. Malgré une bonne centralité d’éloignement moyen certaines villes peuvent être très éloignées de ce point et pourront difficilement être traitées par le médecin. C’est le défaut propre à toute moyenne ! La centralité d’éloignement maximal la plus faible garantit au médecin d’atteindre la ville la plus périphérique facilement, mais il atteindra moins efficacement l’ensemble des autres villes : c’est une position équitable.
Le recours aux indicateurs de centralité issus de la théorie des graphes permettra de conclure de manière plus générale sur la notion de centralité en géographie. Premièrement, on soulignera que la centralité est une caractéristique des lieux relative aux échelles d’observation à travers la comparaison des différents indicateurs de centralité. La centralité de degré qualifie une observation faite au niveau local, qui ne considère que les relations avec les plus proches voisins, alors que les centralités d’éloignement relèvent d’une observation globale du réseau, prenant en compte la totalité des sommets. Deuxièmement, on pourra lever la confusion possible entre centralité de taille (caractérisant la position hiérarchique d’un lieu en termes de concentration de populations, d’équipements etc.) et centralité de réseau (caractérisant l’accessibilité d’un lieu). Ces deux acceptions de la centralité[1] relèvent de deux manières de qualifier la position d’un lieu au sein d’un ensemble : soit par l’observation de sa taille relativement à la taille des autres, soit par l’observation des liens qu’il polarise. Si ces deux acceptions ne sont pas contradictoires car la centralité de réseau et la centralité de taille s’auto-entretiennent, elles relèvent néanmoins de deux manières distinctes de mesurer la centralité.
Pour aller plus loin
1. On pourra réfléchir avec les étudiant·es à définir de nouvelles actions pour lutter contre les épidémies en agissant sur le réseau. Par exemple, on pourra réfléchir à supprimer des liens dans le graphe (fermer des lignes de transport ou fermer des frontières) et à définir dans ce cas quels liens doivent être supprimés en priorité pour endiguer l’épidémie. Couper les liens transatlantiques ou transpacifiques peut diviser le graphe en deux composantes connexes. 2. L’analyse de réseau est mobilisée dans la modélisation de la diffusion épidémique. Dans le cours en vidéo « Réseaux : structures et propagations d’épidémies » (EHESS, 2018), Marc Barthélémy montre comment la structure du réseau influence le seuil de déclenchement d’une épidémie. Les réseaux avec une distribution uniforme de la centralité ont des seuils de déclenchement épidémiques plus élevés que les réseaux très hiérarchisés, où certains nœuds sont en position de carrefour.
[1] « Centralité » in Hypergéo (Pumain, 2004), https://hypergeo.eu/centralite/, consulté le 20/04/2022.
Bibliographie
Oiry A., 2018, « ‘ZAD partout ?’ Jeu de rôle autour du conflit lié au projet d’aéroport de Notre-Dame-des-Landes (Pays de la Loire, France) », Feuilles de géographie, 2018-2, 16 p.
Pumain D., Saint-Julien T., 2010, L’analyse spatiale (1) : Localisations dans l’espace, 2e édition, Cursus-géographie, Armand-Colin, Paris.
Ter Minassian, H., Rufat, S. 2008. « Et si les jeux vidéo servaient à comprendre la géographie ? », Cybergeo : European Journal of Geography [En ligne], consulté le 09 juillet 2021. URL : http://journals.openedition.org/cybergeo/17502 ; DOI : https://doi.org/10.4000/cybergeo.17502.
Sitographie
Grasland, C. 2000. « Graphes et réseaux ». http://grasland.script.univ-paris-diderot.fr/go303/ch2/doc_ch2.htm, consulté le 01.10.2021.
Groupe fmr (flux, matrices, réseaux), https://groupefmr.hypotheses.org/, consulté le 01.10.2021.
EHESS. (2018, 2 mars). Réseaux : structures et propagations d’épidémies. [Vidéo]. Canal-U. https://www.canal-u.tv/73153. Consultée le 20 avril 2022.